
11 заданий на ЕГЭ по базовой математике, которые лучше решить в первую очередь
Базовую математику сдают школьники, которым она не нужна для поступления в вуз.
Если успешно — хотя бы на тройку — сдать базу и пройти минимальный порог по русскому языку, получите аттестат и окончите школу. Расскажем, как справиться с экзаменом.
Как проходит экзамен
В ЕГЭ по базовой математике 21 задание, сам экзамен длится три часа. Для решения первых 15 заданий достаточно знаний за 5—9 класс, для оставшихся — за 10 и 11 классы. Чтобы получить тройку, хватит семи правильных ответов, для четверки — 12, для пятерки — 17.
За каждое задание дают один первичный балл, поэтому неважно, какие именно задачи решать. Но практика показывает, что в экзамене есть задачи, которые правильно решают большинство учеников. Мы выбрали 11 штук — если решить любые семь правильно, экзамен засчитают как успешный. Примеры брали с сайта «Решу ЕГЭ» и из разных сборников.
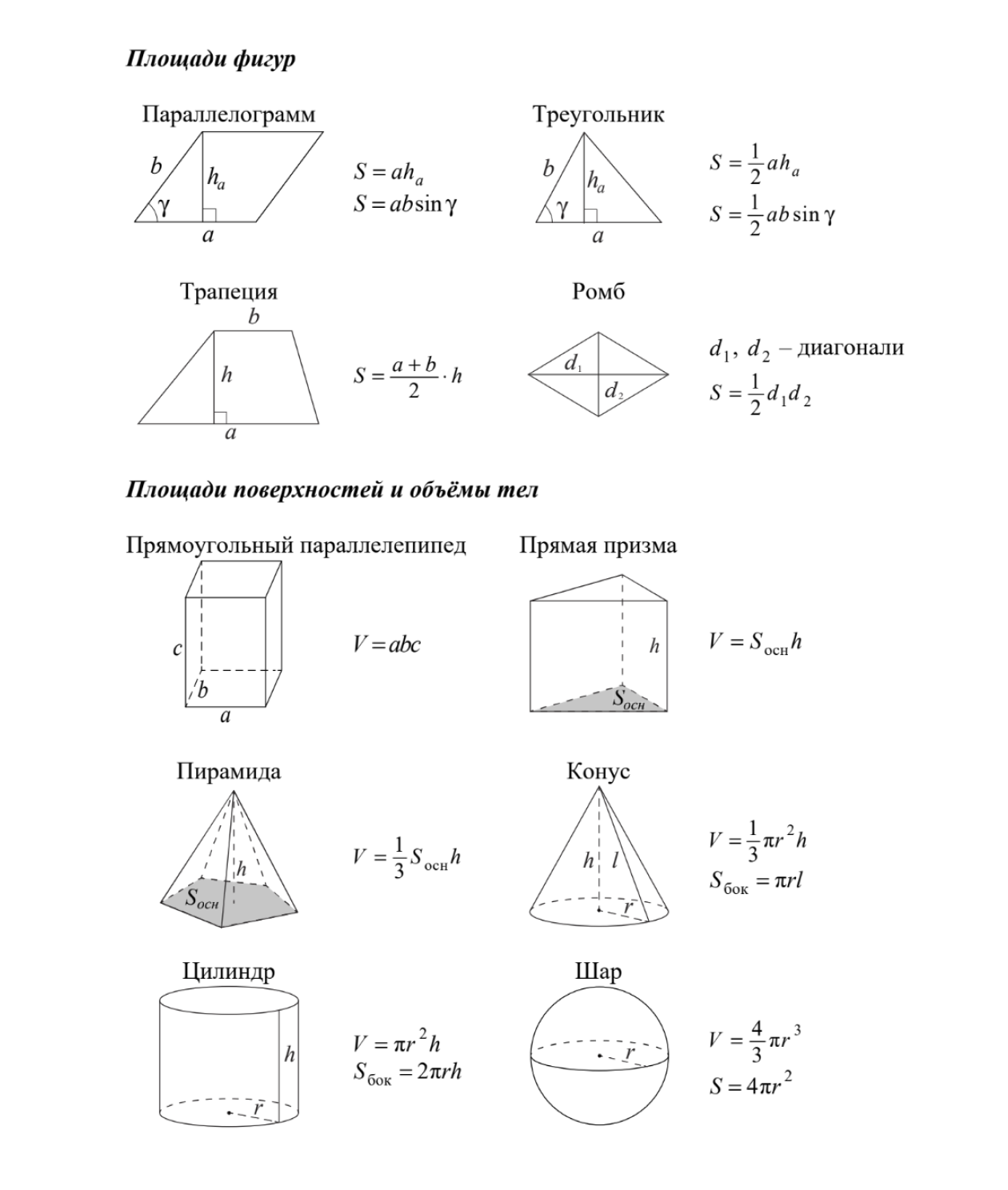
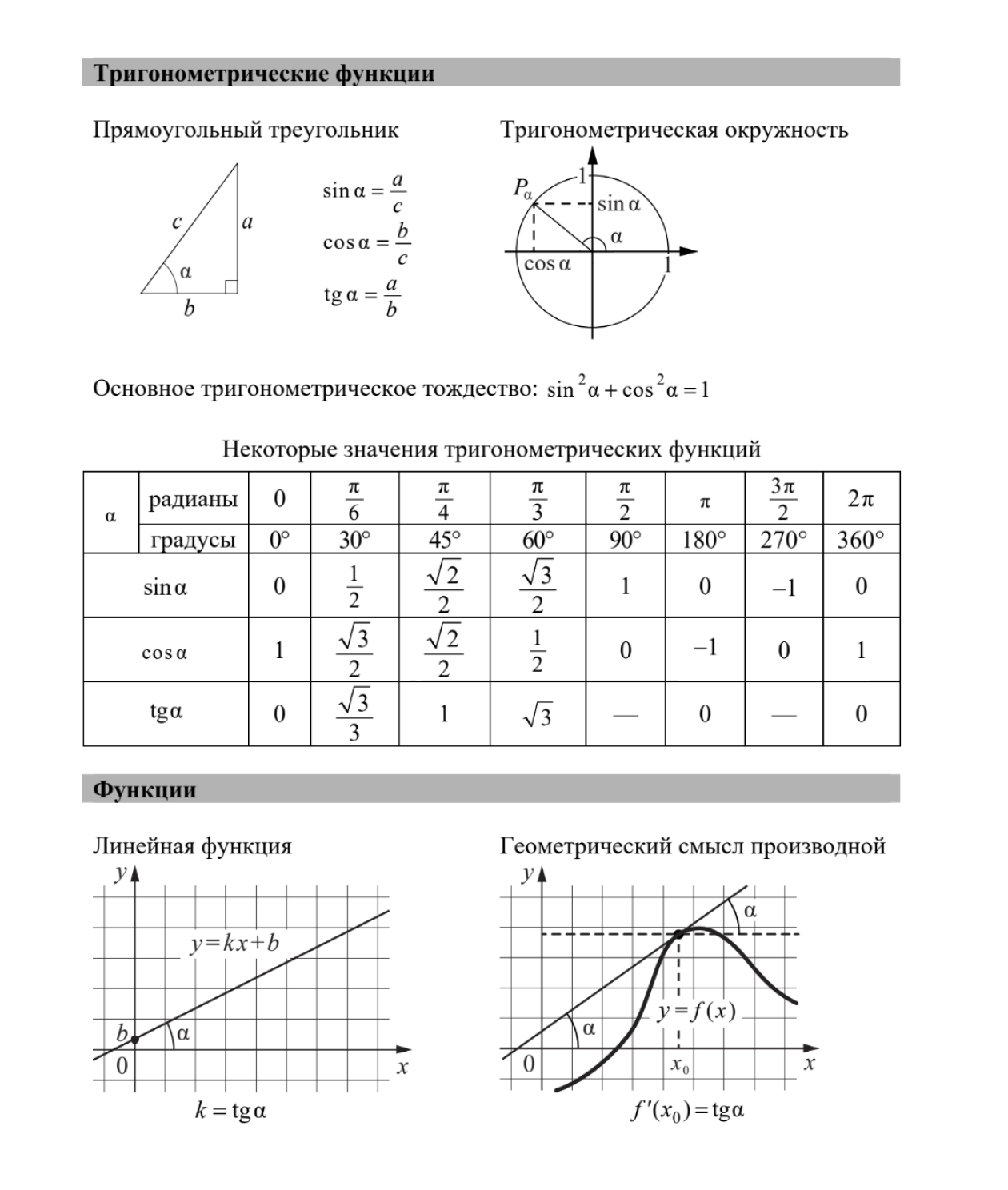
Повысить шансы на успех помогут справочные материалы, которые выдают вместе с заданиями: там есть таблица квадратов, формулы на площади фигур, свойства степеней и логарифмов. Мы будем ссылаться на них в тексте. Если времени для подготовки не осталось, обязательно положитесь на справку.


Первое задание
Проверяет умение пользоваться математическими знаниями на практике. В задачах просят найти количество машин для перевозки определенного числа пассажиров, количество товара, приобретаемого на конкретную сумму, и так далее. С подобными заданиями ребята сталкиваются уже на ОГЭ по математике в девятом классе.
Как решать. Для правильного выполнения задачи нужно:
- Помнить, как переводить массу, стоимость, время и расстояние из большей единицы измерения в меньшую и наоборот — например, килограммы в граммы.
- Знать правила округления чисел, понимать, в каком случае брать ответ с избытком, а в каком — с недостатком.
- Представить ситуацию из задачи или вспомнить такую же ситуацию из жизненного опыта.

Второе задание
Задача-тест на сопоставление величин, их возможных значений.
Как решать. Ответить помогут жизненный опыт и знания величин:
- В условии зафиксируйте, какая единица измерения самая большая, а какая — самая маленькая.
- Линиями соедините величину и ее значение.
- Если трудно оценить какую-то величину, работайте с остальными. По остаточному принципу оцените трудную величину. Ответ записывайте, только когда сопоставите все величины.

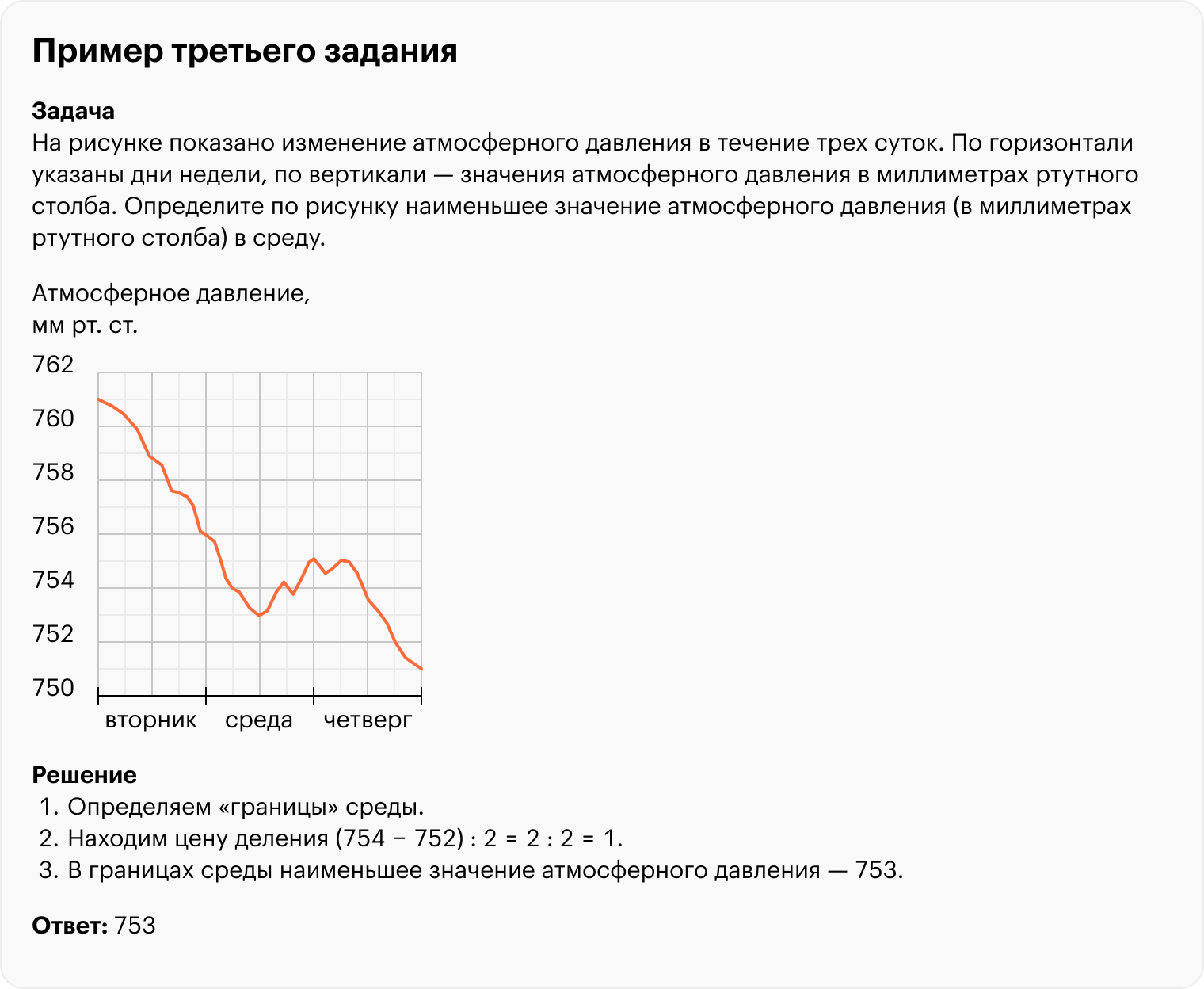
Третье задание
Проверяет умение работать с информацией в виде диаграмм, графиков и таблиц.
Как решать. При работе с диаграммой или графиком:
- Обратите внимание, значение какой величины откладывают по горизонтали, а какой — по вертикали.
- Поймите, что использовать при ответе на вопрос: весь график целиком или его часть.
- Подсчитайте, чему равен шаг между делениями на графике, — это позволит оценить цену деления.
- Обратите внимание на слова «более», «не более», «менее», «не менее»: например, не более трех — это три и все, что меньше.
Четвертое задание
Смотрят на умение вычислять и преобразовывать выражения.
Как решать. Для выполнения задания нужно:
- Знать правила сложения, вычитания, умножения и деления целых чисел и дробей.
- Уметь сопоставлять величину и ее числовое значение.
- Подставлять числовые значения величин в формулы.
- Выражать неизвестный компонент из формулы.
- Устанавливать последовательность применения формул в задании, если их две и более.
Если трудно выразить неизвестную величину, подставьте в формулу все известные значения. У вас получится уравнение, решив которое, вы найдете нужную величину.

Пятое задание
Здесь вычисляют вероятности событий в простейших случаях.
Как решать. Нужно знать как минимум формулу классической вероятности: Р(А) = m/n, где m — количество благоприятных событий, n — количество всех событий.
Важно внимательно прочитать вопрос в задаче и четко понять, вероятность какого события просят найти. Ответ будет достоверным, если он начинается с ноля целых: например, 0,3 или 0,25.
Еще обратите внимание, просят ли округлить ответ, и если да, то до каких долей: десятых, сотых.

Шестое задание
В задаче извлекают информацию из таблиц, диаграмм и графиков, по условию выполняют действия с полученными данными.
Как решать. Нужно хорошо уметь считать. Жизненный опыт и наблюдения ускорят процесс решения.
Прежде чем записывать данные, проверьте, что именно просят внести в ответ.

Восьмое задание
В этом задании придется доказательно порассуждать.
Как решать. Внимательно читайте условие задачи и варианты приведенных утверждений.
Запишите краткое условие задачи в форме, удобной для понимания. Чаще это рисунок. Каждый вариант ответа сопоставьте с условием, не домысливая факты.
Если умеете выполнять действия над множествами, это задание легко решается с помощью кругов Эйлера. Систематическое прорешивание заданий тренирует логику.

Девятое задание
Задача, при решении которой необходимо умение использовать теоремы планиметрии, оценивать размеры объектов окружающего мира.
Как решать. Вот несколько советов:
- В зависимости от условия задачи можно воспользоваться формулами из справочного материала по геометрии: площади плоских фигур, формулы для нахождения длины средней линии треугольника и трапеции и так далее.
- Пригодится умение разбивать фигуры на прямоугольные треугольники, квадраты, прямоугольники, трапеции.
- Повторите понятие масштаба и свойства площадей.
- Если в задаче речь о плане местности, для решения можно использовать прием «собирание целой клетки». Прикиньте количество клеток, заполненных целиком, и количество неполных клеток — и только потом приступайте к вычислениям по вопросу задачи.
- Обращайте внимание на размеры клетки или квадрата.
- Освежите в голове правила округления чисел.

Четырнадцатое задание
В условии попросят вычислить и преобразовать выражения.
Как решать. Вот что нужно:
- Знать, как выполнять действия с десятичными и обыкновенными дробями, смешанными числами, с положительными и отрицательными числами.
- Уметь переводить смешанные числа в неправильные обыкновенные дроби, обыкновенную дробь — в десятичную.
- Уметь расставлять порядок действий.

Шестнадцатое задание
Задание на нахождение значения выражения. Вариантов много, задачи со степенями, корнями, логарифмами можно решить по формулам из справки.
Как решать. В справочных материалах есть формулы для упрощения логарифмических выражений, выражений со степенями.
Если в задаче будет тригонометрия, формул из справочного материала может не хватить. Поэтому повторите, как из основного тригонометрического тождества выразить одну тригонометрическую функцию через другую и как пользоваться тригонометрической окружностью.
Чтобы выполнить задание, нужно знать свойство умножения и сложения, уметь раскрывать скобки.

Семнадцатое задание
Проверяет умение решать рациональные, иррациональные, показательные, тригонометрические, логарифмические уравнения.
Как решать. Что пригодится при решении:
- Алгоритмы решения уравнений.
- Умение выполнять действия с числами.
- Помнить, что в логарифмических и иррациональных уравнениях нужно делать проверку — хотя бы в уме — или находить область определения.
В справочном материале есть формулы для решения квадратных, логарифмических и показательных уравнений.
Если при решении уравнения вы получили два или более корня, а в задании нет дополнительных условий для записи ответа, обязательно перепроверьте себя. Тогда поймете, какой корень посторонний, а какой записать в ответ. В задании в ответ пишут одно число.

Как дотянуть до четверки
Если хорошо решаете неравенства, посмотрите на 18-е задание: обычно там просят установить соответствие между неравенствами и их решениями или связь между точками на координатной прямой и их координатами.
Еще обратите внимание на 12-е задание — оно по геометрии. Формулы будут в справочном материале, найдите нужную и попробуйте подставить значения.
Если в дополнение к перечисленным 11 задачам верно решите одно из этих двух или других оставшихся, получите четверку.
Новости из мира образования, советы по карьере и учебе, вдохновляющие истории — в нашем телеграм-канале: @t_obrazovanie



















