«Трудно учиться по хорошей, но скуч­ной книге»: как я пишу учебники по геоме­трии

Я преподаю математику уже четверть века.

За эти годы я понял, что разумные дети чем-то похожи на древних греков: они знают не больше эллинов, но так же пытливы от природы. Математика для них — игра познания. Один мой ученик сформулировал это лучше: «Математика — искусство так упрощать мир, чтобы его можно было понять». Я горжусь этой формулой и стараюсь ей следовать.

Задачки по геометрии я придумывал с самого начала: для уроков, контрольных работ, турниров и олимпиад. Потом составил из них книжку — она оказалась востребована школьниками и учителями и выдержала уже пять изданий. Наверное, пришло время делиться опытом, и за последние годы я написал свой учебник по геометрии. Он получился красивым, во многих смыслах новым, а главное — интересным.

Расскажу, как мне удается увлекать детей математикой, писать книги и задачи для олимпиад.

Я учился в обычной московской школе рядом с домом, получал там свои четверки и пятерки, но особой любви к точным наукам не питал. Гораздо больше меня привлекали физкультура и география. На математику вообще ходил без удовольствия: мне не нравилась учительница.

В шестом классе мой друг, лучший ученик параллели, собрался поступать в школу № 57 — в ней были профильные физико-математические классы с сильными преподавателями. Я решил тоже попробовать свои силы, можно сказать, из спортивного интереса.

Но вступительный экзамен оказался сложным. Мой друг его сдал, а я завалил. Тогда он мне сказал: «Иди туда на кружок — станешь таким же умным, как я». Конечно, я обиделся, но весь следующий год ходил на вечерние курсы при 57-й школе. Там я осознал, что математика — это понятно, полезно и, главное, интересно. А потом легко сдал экзамен.

В 57-й школе мне очень повезло: я попал в класс к прекрасному учителю — Рафаилу Калмановичу Гордину. Именно он привил мне на всю жизнь любовь к геометрии. Кстати, свою первую олимпиадную задачу я придумал еще в школе, ее опубликовали тогда в журнале «Квант».

Моя сестра — кандидат наук, ее муж — профессор физики, оба — преподаватели Московского университета. Они на пару убедили меня поступить на физический факультет МГУ. Сам я тогда еще точно не знал, чем хочу заниматься в будущем, и послушал их совета.

Преподавать я начал на пятом курсе, вместе с друзьями. Это была середина 90-х — сложное время, приходилось заниматься репетиторством. В «Пятьдесят седьмой» как раз искали преподавателей для вечерних курсов, и нас взяли.

Мы целый год готовили ребят к поступлению в школу и, думаю, неплохо делали свое дело. Хотя опыта было мало: помню, просил учеников называть меня только по имени — стеснялся, когда ко мне обращались по отчеству. А ведь хороший учитель должен не только уметь все объяснить, рассказать анекдот, когда нужно, но при этом еще и держать дистанцию с учениками и следить за обратной связью. Я тогда не совсем с этим справлялся.

Часто я объяснял математические концепции с точки зрения физики. Всегда интересно посмотреть на предмет с другой стороны. Например, медианы треугольника пересекаются в центре его масс — так в геометрии работает правило рычага. Угол падения луча света на зеркало равен углу его отражения — здесь действует принцип наименьшего времени Пьера Ферма. И так далее.

Я с головой ушел в преподавание: получал огромное удовольствие от работы и видел результаты своего труда. Потом уже в 710-й школе я вел два класса: один самостоятельно, а в другом сотрудничал с замечательным учителем — Евгением Абрамовичем Бунимовичем. И тем не менее первые три года я каждое лето задавался одним и тем же вопросом: продолжать ли дальше?

В 90-е статус учителя был низким, а зарплаты крошечными. Один мой одноклассник, став тогда бухгалтером, очень гордился своей профессией. Я же стеснялся говорить, что работаю в школе. Но преподавать все равно продолжал: считал это важным социальным делом.

Через некоторое время мне поручили сложный класс, где учились не слишком мотивированные дети. Преподаватели работали с ним «вахтовым методом» — каждый по три месяца. Выдержать целый год было трудно.

Помню, что за одну контрольную почти весь класс получил двойки, но при этом никто из этих ребят не расстроился. Я разобрал все задачи и предложил им после урока написать в точности то же самое. Это вызвало некоторое замешательство — исправить свои оценки можно было так просто… Но природа — или привычка — взяла верх, и после урока мальчишки радостно побежали играть в футбол.

Выдающихся результатов за те три месяца я не добился, но понял главное: в обычной школе преподаватель в первую очередь должен держать дисциплину — профессиональные умения здесь отходят на второй план. Поэтому в учительской среде так ценят педагогический стаж: если за 20 лет дети не съели преподавателя, это уже многое о нем говорит.

Первый задачник. С самого начала преподавания я стал придумывать задачи и делать из них подборки на листочках, которые раздавал на уроке. Это распространенная практика среди учителей: каждый хочет построить свою систему, а не идти по чужим шаблонам.

Составлять задачи — это искусство. В некоторых учебниках просят по двум катетам найти гипотенузу, и таких заданий там больше половины. Геометрическая суть их лишь в том, чтобы ученик не перепутал термины. Я считаю, что даже в самых простых упражнениях должна быть какая-то математическая идея, пища для детских мозгов.

Вот пример простой, но при этом нестандартной задачи на теорему Пифагора. У Пети есть квадратный лист тонкой фанеры площадью 5 м². Ему нужно пронести его через дверной проем, ширина и высота которого 80 и 210 см. Пройдет такой лист в дверь или нет  ?

Или другой пример. Приблизительно на сколько километров удалена линия горизонта от взрослого человека, стоящего на берегу моря? Чтобы ее решить, нужно знать только радиус Земли и теорему Пифагора  .

Примерно 10 лет назад в Центре непрерывного математического образования Иван Валерьевич Ященко увидел мои листки с заданиями, которые я накопил за 15 лет работы в школах, и предложил издать их в виде книги. Так появилось мое первое пособие «Уроки геометрии в задачах». Интересно, что даже рисунок на его обложке я сделал из четырех задач этой книги.

Цифровой учебник. В 2018 году в Москве стартовал проект «Математическая вертикаль»  , и для него были нужны новые учебные пособия. Изначально предполагалось, что над учебником будет работать большая группа авторов, а мне предложили написать только один параграф, чтобы на него ориентировались другие. В итоге вышло так, что из коллектива авторов остался я один, и, пожалуй, книга от этого только выиграла.

Я изучил множество российских учебников по геометрии. Все они были неплохи, но дети занимались по ним без удовольствия. Трудно заставить учиться по хорошей, но скучной книге. Очень важен язык, которым она написана. Поэтому я взял за образец стиль Михаила Гаспарова  , автора «Занимательной Греции»  . Нужен был легкий слог, щепотка юмора и никакого академизма.

Как и на своих уроках, любую тему в учебнике я начинал с объяснения того, как она связана с окружающим нас миром, и лишь затем давал теорию и задачи. Думаю, в наше время это правильный подход.

Сегодня любые формулы и факты можно легко найти в поисковике интернета. А вот работать с этими фактами, анализировать их и видеть связи между ними нужно уметь.

Сначала я разбираю теорию на пальцах и примерах из жизни, только потом мы даем определения и разбираем доказательства. Мой подход заключается в том, чтобы идти от простых заданий к сложным, от накопленного опыта — к общей теории. Это классическая схема. Дети в основном учатся по аналогии, поэтому им нужно много простых примеров и упражнений. А потом уже можно постепенно усложнять.

Для книги я подобрал и составил много хороших задач, разбитых по трем уровням сложности. И в каждом параграфе их больше, чем требуется для урока. В этом смысле мой учебник похож на супермаркет: хороший учитель найдет там все необходимое и отберет по своему вкусу.

Бумажная версия. Первый вариант учебника вышел в цифровом формате в 2018 году. А уже в августе 2019 издательство «Просвещение» сообщило, что хочет опубликовать книгу на бумаге. Новость отличная, но было одно «но»: готовый вариант ждали через месяц. Пришлось все делать в авральном режиме: верстать сложный макет, чертить множество рисунков, решать вопросы с авторскими правами на фотографии.

Неожиданно возникли сложности с цензурой. Например, в одной из глав описывалась хорошо известная история про Архимеда, который открыл знаменитый закон гидростатики, находясь в общественной бане. Увидев, как его тело вытесняет воду из ванны, он мгновенно понял, что так же можно высчитать объем золотого венца, который ему поручил исследовать правитель Сиракуз. В восхищении Архимед закричал «Эврика!» и выбежал голым на улицу.

Прочитав это место, редактор попросил меня убрать из текста слово «голый». Не помогла и более нейтральная формулировка «выбежал не одеваясь». Мне ответили, что это тоже недопустимо, ведь ученики могут догадаться, что ученый был голым. Это правда: дети вовсе не так глупы и вполне могут сделать простой логический вывод. Но если они еще немного интересуются историей, сразу вспомнят, что нагота во времена античности не была столь предосудительной. На древних олимпиадах атлеты соревновались именно в таком виде.

Тем не менее, несмотря на все сложности, мы справились. Мой коллега Иван Валерьевич Ященко собрал замечательную команду и стал главным редактором учебника, а художник Алексей Вайнер сделал чудесные смешные иллюстрации.

После первого издания мы переработали и улучшили учебник: учли пожелания многих учителей, вставили больше упражнений и простых задач. Появились новые схемы доказательств, все решения задач мы разбили на пункты, а к каждому примеру добавили краткую запись его условия. Появились ответы, указатели и многое другое. В таком виде учебник вышел в 2023 году и был награжден премией правительства Москвы.

Времена меняются, а вместе с ними — подходы к образованию. Многие говорят, что в СССР оно было лучше, чем сейчас, и дети тогда учились усерднее. Отчасти это правда: в ту пору не было интернета, современных гаджетов, компьютерных игр и социальных сетей.

Но дело не только в этом. Мне кажется, советские школьники понимали, что учеба — это социальный лифт. Для людей из провинции образование становилось реальной возможностью построить карьеру. Если дворник в Советском Союзе зарабатывал 70 ₽ в месяц, то инженер получал 200 ₽, а у академика от государства была машина, дача и зарплата 500 ₽.

Теперь такой социальный лифт не работает. Сейчас, чтобы получать большие деньги, хорошо учиться вовсе не обязательно — это демонстрируют, например, многие известные блогеры. Но нельзя не заметить, что последние 20 лет сильно возросла потребность в хороших ИТ-специалистах: для всего нужно писать коды, создавать сайты и приложения. И, как следствие, школьники учатся программированию не ради оценок, а для себя. Получается, что сейчас ИТ — это новый социальный лифт.

Я изучил много иностранных учебников и общался с ребятами из разных стран, поэтому неплохо себе представляю, как выглядит обучение математике в Швеции, Финляндии, Франции, Италии, Англии и США. После Второй мировой войны западная система образования разделилась на уровни — теперь там немногие школьники занимаются математикой углубленно и потом становятся инженерами или учеными.

Большинство выбирает для себя легкий путь. Наверное, поэтому из общих образовательных программ британских учебников исчезли все доказательства и остались однотипные упражнения на применение формул. Откуда эти формулы берутся, никто не объясняет. Получается, что математику в средних школах там изучают по принципу готовых рецептов — примерно так, как это делали жрецы Вавилона и Египта еще до возникновения греческой науки.

В школах России точные науки пока преподают более углубленно, с подробными объяснениями и сложными задачами. Конечно, у такого подхода есть и свои минусы. В любом классе найдутся ребята, которым тяжело дается абстрактное мышление, — это хорошо заметно, например, по тому, как они понимают рассуждение от противного. Чтобы у таких учеников не было отвращения к предмету, надо искать новые подходы.

На уроках теперь можно использовать видео и другие интерактивные элементы — например, при изучении теоремы учителю проще включить ролик, где доказательство подается с анимацией. Также на компьютере легко сделать простые тесты, которые можно быстро пройти и сразу получить обратную связь.

Есть и другие способы оживления абстрактных понятий. Например, детей привлекают наглядные модели. Я часто использую мыльные пленки или конструктор из магнитных шариков и палочек — их можно потрогать или собрать из деталей пространственную фигуру. Когда человек держит такую вещь в руках, это вызывает совсем другие ощущения.

Часто я придумываю задания для таких моделей: найти высоту пирамиды или другой пространственной фигуры. Можно задать вопрос о жесткости такой конструкции и потом сразу проверить ответ на практике.

Есть потрясающие вещи, которые интересны всем детям. Один из таких примеров — параболическое зеркало. Оно собирает лучи света в одну точку — фокус — и там концентрируется большая энергия.

Для демонстрации этого явления я как-то поставил два зеркальных параболоида напротив друг друга на расстоянии 5 м. В фокусе одного из них была галогеновая лампочка, другого — зажим для бумаги. Несмотря на то что тепло от лампочки не ощущалось даже на расстоянии 30 см, бумага в фокусе другого параболоида сразу начала дымиться. И хотя сработала пожарная сигнализация, дети были в полном восторге. К сожалению, эти зеркальные параболоиды нам пришлось заказывать из Южной Кореи, у нас их пока не производят. Правда, такие отражатели еще можно достать из старых прожекторов.

Есть и другие модели, которые не оставят детей равнодушными: эллиптический бильярд, тенсегрити  , велосипед на квадратных колесах, который ровно едет по круглым бревнам.

В России такие приспособления делают пока только в двух местах: в Мастерской науки Евгения Ширяева при Политехническом музее в Москве и в Институте имени Стеклова у прекрасного популяризатора математики Николая Андреева. Но производятся они чаще всего в единственном экземпляре и стоят дорого, поэтому учебные заведения не готовы их покупать.

Сейчас я работаю в двух московских школах с углубленным изучением математики: в «Пятьдесят седьмой» и лицее «Вторая школа». Также преподаю в маленькой хорошей частной школе ЦПМ. Кроме того, веду занятия онлайн по своему учебнику для русскоговорящих ребят из Китая, Италии, Австралии, Сербии.

В свободное от работы время я придумываю задачи для сборников ЕГЭ и многих олимпиад: Московской, «Курчатов», Турнира городов. А еще я сочиняю стихи и песни, записываю музыку, выступаю с концертами. В 2020 году издал книгу стихов «Техника акварели».

С прошлого года веду свой канал в «Телеграме»: там я выкладываю свои новые задачи, материалы для контрольных работ, делаю анонсы своих выступлений и отвечаю на вопросы читателей.

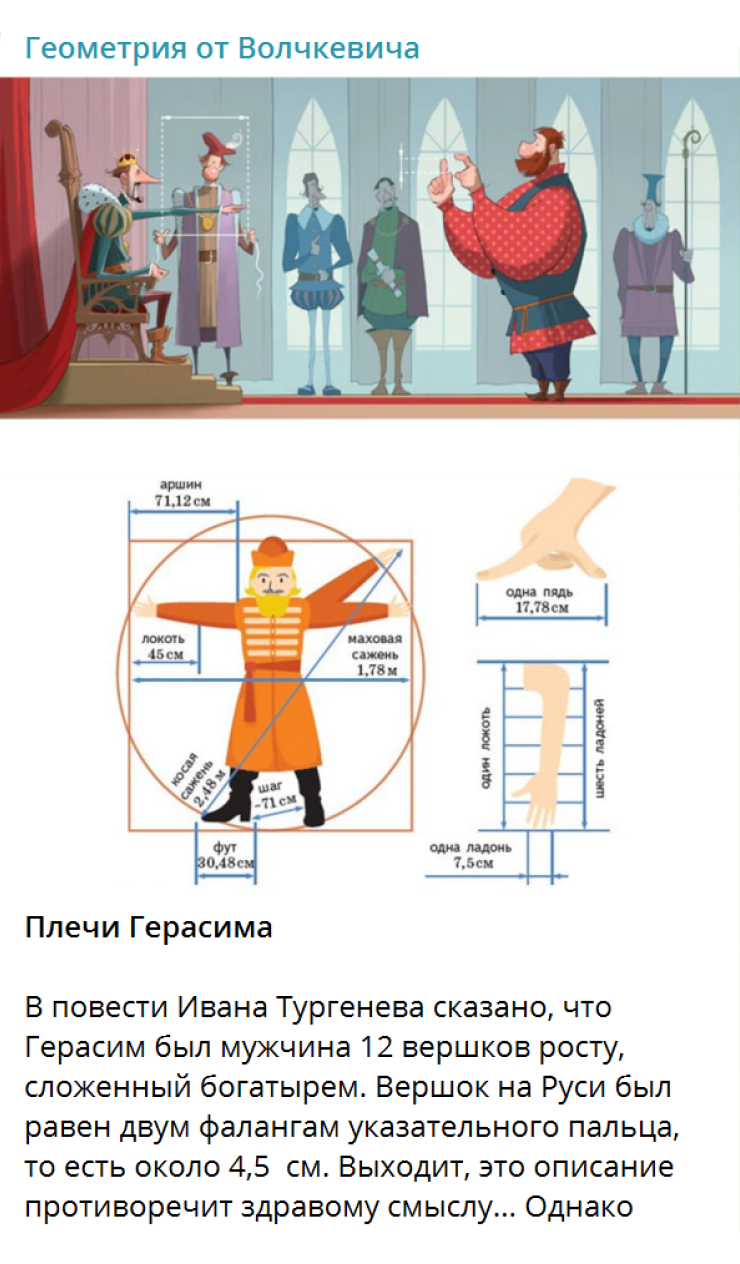
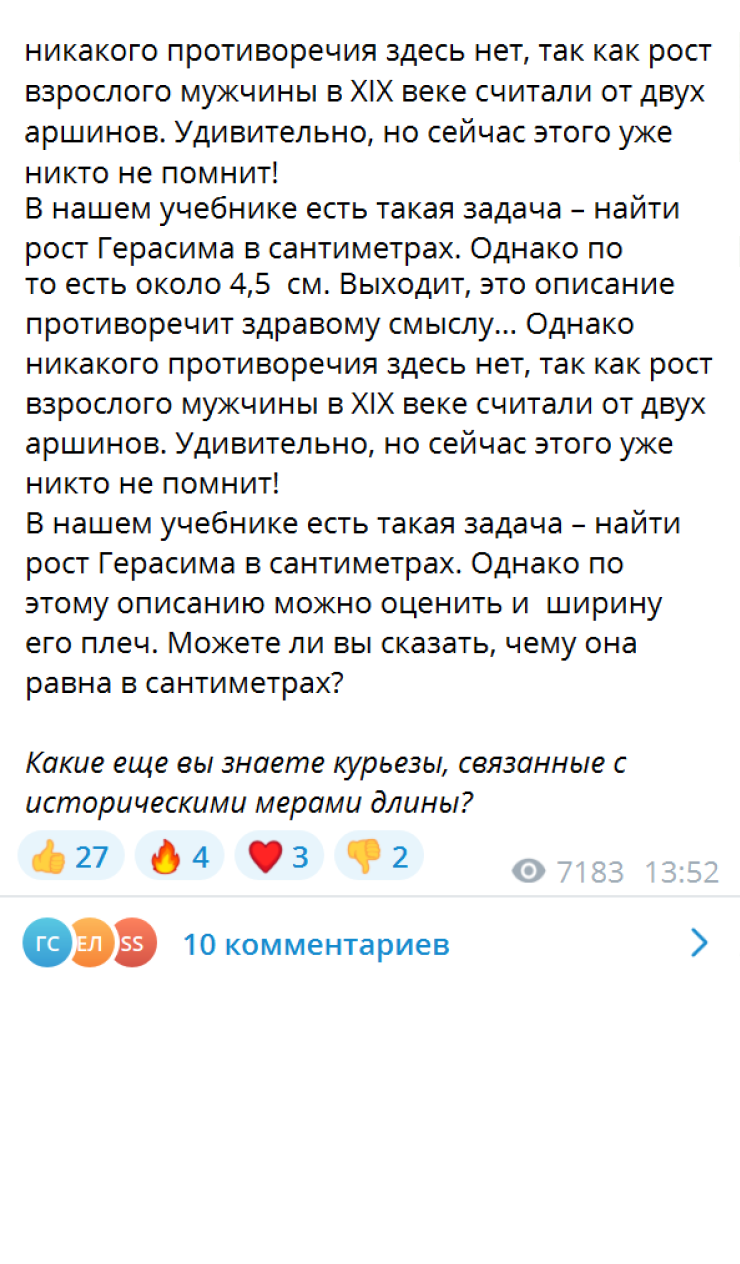
В ближайшее время я начну писать учебник по стереометрии. У меня уже есть свой хороший курс для математических классов, который я веду много лет. Очевидно, что для обычных школ его придется упрощать.

В любом случае я хотел бы, чтобы геометрическая теория в моем пособии не была оторвана от окружающего мира, шла рядом с физикой, химией или даже изобразительным искусством. Российский математик Владимир Арнольд говорил, что математика — это часть физики. Я бы продолжил его мысль: математика — это абстрактная часть любой точной науки. С ее помощью можно решать любые задачи, если правильно упростить их до математических моделей. В этом смысле математика действительно царица наук: она связывает их в одно целое.