Как грамотно составить инвестиционную стратегию

Если вас не напугал подзаголовок, углубимся в портфельную теорию и разберем, как оптимизировать инвестиционную стратегию.
На фондовом рынке много факторов, влияющих на поведение активов, — как макроэкономических, так и свойственных отдельным секторам и компаниям.
Например, финансовый отчет компании может разочаровать инвесторов — и котировки ее акций рухнут.
Изначально нельзя предугадать все факторы, поэтому рынку свойственна неопределенность и риски. В этой статье рассмотрим, как можно снизить их, при этом не сильно потеряв в доходности.
Алгоритм действий следующий:
- Отберем оптимальные портфели на основе классического подхода Марковица.
- Составим матрицу выигрышей на основе критерия эффективности Шарпа.
- Найдем показатели эффективности по критерию Вальда.
- Рассчитаем матрицу рисков и определим цену игры по критерию Сэвиджа в чистых стратегиях.
- Свяжем критерии Вальда и Сэвиджа.
- Определим приоритетную последовательность инвестиционных портфелей.
Поиск оптимального портфеля
Ключевой способ снизить риски при инвестициях — диверсификация. Ее суть заключается в том, что деньги распределяются между различными классами активов, а также между активами внутри одного класса.
Например, вы не вкладываете все деньги только в акции, но также инвестируете в облигации и золото. А набор акций распределяете по разным странам и секторам экономики.
В этом отношении инвестору могут помочь ETF — фонды, которые уже состоят из широкой корзины активов. Например, купив пай фонда FXUS, можно разом вложиться в более чем 500 американских компаний из 11 секторов экономики.
Подобное распределение по многим активам позволяет устранить специфические риски — связанные с конкретной компанией или отраслью. Остается только рыночный риск, который нельзя исключить.
Ведь всегда может произойти природный катаклизм, геополитическое событие или появится новый штамм коронавируса, который приведет к панике на фондовом рынке. В этом случае портфель инвестора, скорее всего, уйдет в просадку. Весь вопрос — насколько сильную.
Таким образом, грамотная диверсификация позволит уравновесить портфель и не даст ему сильно просесть в кризис. Принципы диверсификации заложил в 1952 году Гарри Марковиц, предложив миру современную теорию портфеля.
Современная теория портфеля. Основная ее мысль заключается в том, что на фондовом рынке доходность и риск взаимосвязаны.
При этом доходность актива выражается в так называемом математическом ожидании, а риск — в стандартном отклонении доходности. Стандартное отклонение показывает, насколько доходность актива или портфеля может отличаться от его средней доходности. Чем выше стандартное отклонение, тем сильнее разброс возможных результатов и тем выше риск. Простой пример расчета стандартного отклонения можно найти в статье про всепогодную стратегию.
Если говорить совсем просто, мерой риска на рынке выступает волатильность — насколько капризно ведет себя актив. Именно поэтому акции, которые по своей природе более волатильны, считаются рисковым вложением, а облигации — относительно безопасным. Ведь последние предлагают прогнозируемую доходность и их цена колеблется не так сильно.
Что же касается математического ожидания, простыми словами — это средний результат или значение показателя, который можно получить при прочих равных условиях.
Среднюю ожидаемую доходность портфеля мы можем посчитать, умножив вес каждого актива на его доходность.
- Например, мы имеем портфель, который состоит из активов А и В в пропорции 50/50. При этом ожидаемая доходность актива А равна 10%, а В — 15%. Таким образом, средняя ожидаемая доходность портфеля: 0,5 × 10 + 0,5 × 15 = 12,5%.
Современная теория портфеля утверждает, что для каждого набора активов существует оптимальная смесь, которая дает лучшую доходность при заданном риске. Такой портфель считается оптимальным. А все множество оптимальных портфелей образуют так называемую эффективную границу. К этому понятию мы вернемся чуть позже — и даже нарисуем, как она выглядит.
Сейчас же, чтобы понять, за счет чего работает диверсификация, обратимся к другому понятию — корреляции. Она показывает степень взаимозависимости активов в портфеле на конкретном историческом отрезке. При этом значения коэффициента корреляции могут быть от −1 до +1.
Если два актива движутся синхронно, коэффициент корреляции будет ближе к +1. Если в противоположных направлениях — ближе к −1. А если корреляция близка к нулю, значит, взаимосвязи почти нет. То есть при росте или падении одного актива другой может никак себя не проявлять.
Например, корреляция акций и облигаций на рынке США в период с 1950 по 2012 год была 0,11. Это значение ближе к 0, чем к 1, поэтому оба инструмента исторически служат отличным диверсификатором друг для друга. И, например, добавив 10% акций к портфелю из облигаций, зачастую можно не только повысить ожидаемую доходность, но и снизить риск портфеля.
Подведем подытог: диверсификация портфеля достигается за счет подбора активов со слабой и обратной корреляцией друг к другу. В этом случае движение цены одного актива будет компенсироваться движением цены другого. Например, ваши акции упали, а золото выросло в цене — просадка по всему портфелю будет ниже, чем если бы ваш портфель состоял целиком из акций.
С теорией закончили, теперь перейдем к практике. Возьмем две условные акции и составим для них оптимальный портфель.
Поиск оптимального портфеля классическим методом по Марковицу
Возвращаясь к теории Марковица, следует отметить, что она подразумевает некоторые допущения:
- Финансовый рынок обладает высокой ликвидностью, то есть любой актив можно быстро и в любом объеме реализовать на рынке. В действительности же на рынке далеко не у всех ценных бумаг высокая ликвидность. Например, есть акции третьего эшелона, по которым проходит низкий объем торгов. Тем не менее для голубых фишек предположение справедливо.
- Не учитываются транзакционные издержки и налоги. На деле же издержки в долгосрочной перспективе могут сильно повлиять на итоговую доходность. Об их оптимизации можно прочитать в статье «4 правила успешного инвестирования».
- Рынок эффективен — то есть вся возникающая информация немедленно и в полном объеме отражается в стоимости активов. В действительности на рынке существует информационная асимметрия — например, кто-то обладает инсайдерскими данными.
В процессе дальнейшего анализа мы будем исходить из перечисленных допущений.
В качестве примера мы соберем примитивный портфель из акций двух российских компаний: ПАО «Русгидро» — HYDR и ПАО «Лукойл» — LKOH. Весь алгоритм расчета я представил в гугл-таблице.
Для начала скачаем данные котировок с сайта mfd.ru — я взял дневную доходность акций за период с 14.01.2015 по 03.04.2020.
Затем посчитал дневную логарифмическую доходность для каждой акции. Это делается, чтобы сгладить сильные колебания цены в течение каждого дня и сделать данные более симметричными, что улучшает точность расчета.
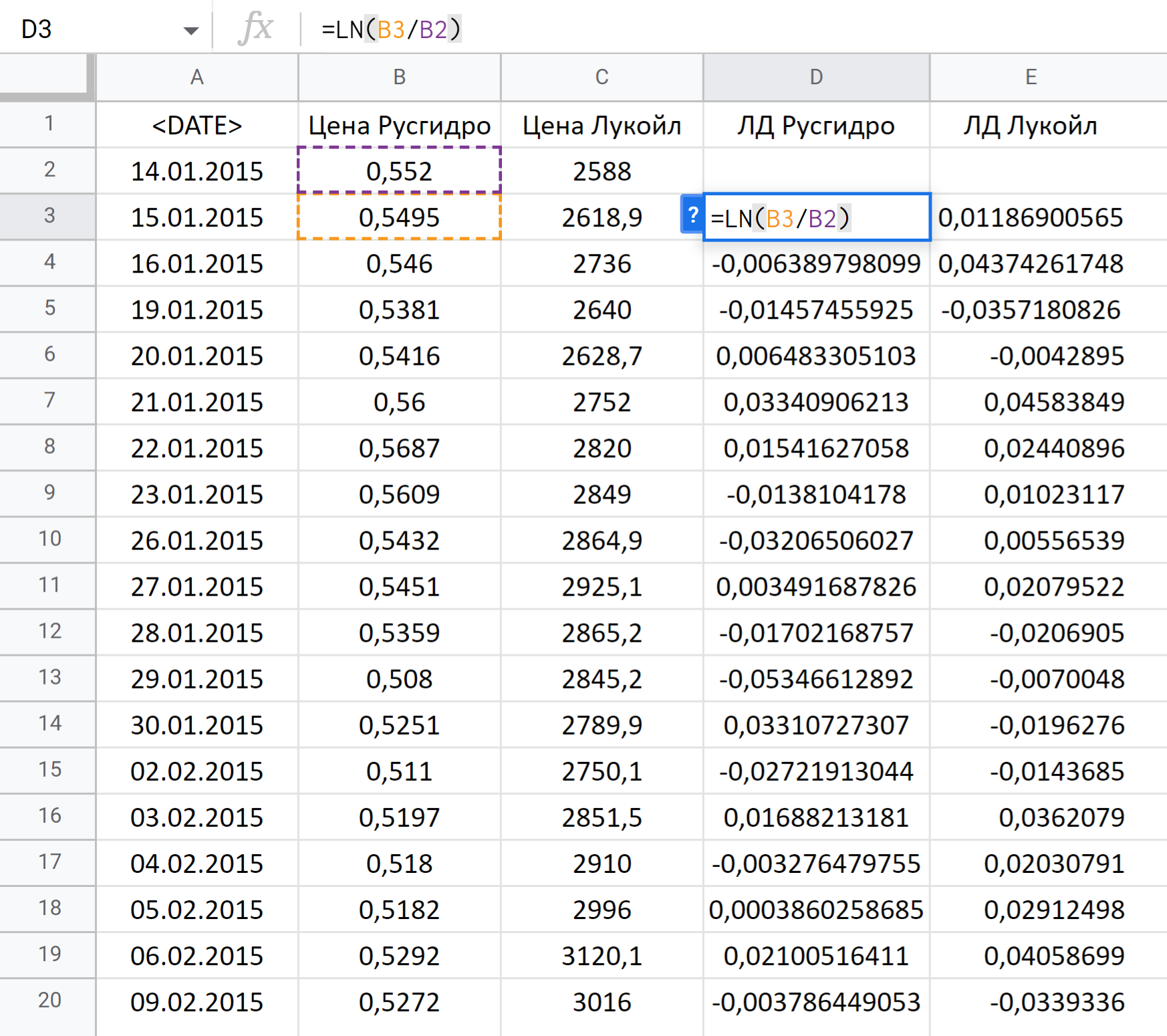
Описательная статистика. Теперь мы можем посчитать ожидаемую доходность каждой бумаги, то есть среднее значение из всех рассчитанных доходностей за период по ценной бумаге, и ее риск — стандартное отклонение и дисперсию.
Дисперсия — это мера разброса доходности актива от ее среднего значения. Уровень разброса доходности напрямую связан с уровнем риска. Чем больше дисперсия, тем капризнее актив и выше риск. Для этого воспользуемся встроенной программой в «Описательная статистика» в «Экселе». Результатом будет таблица с показателями на основе наших исходных данных.
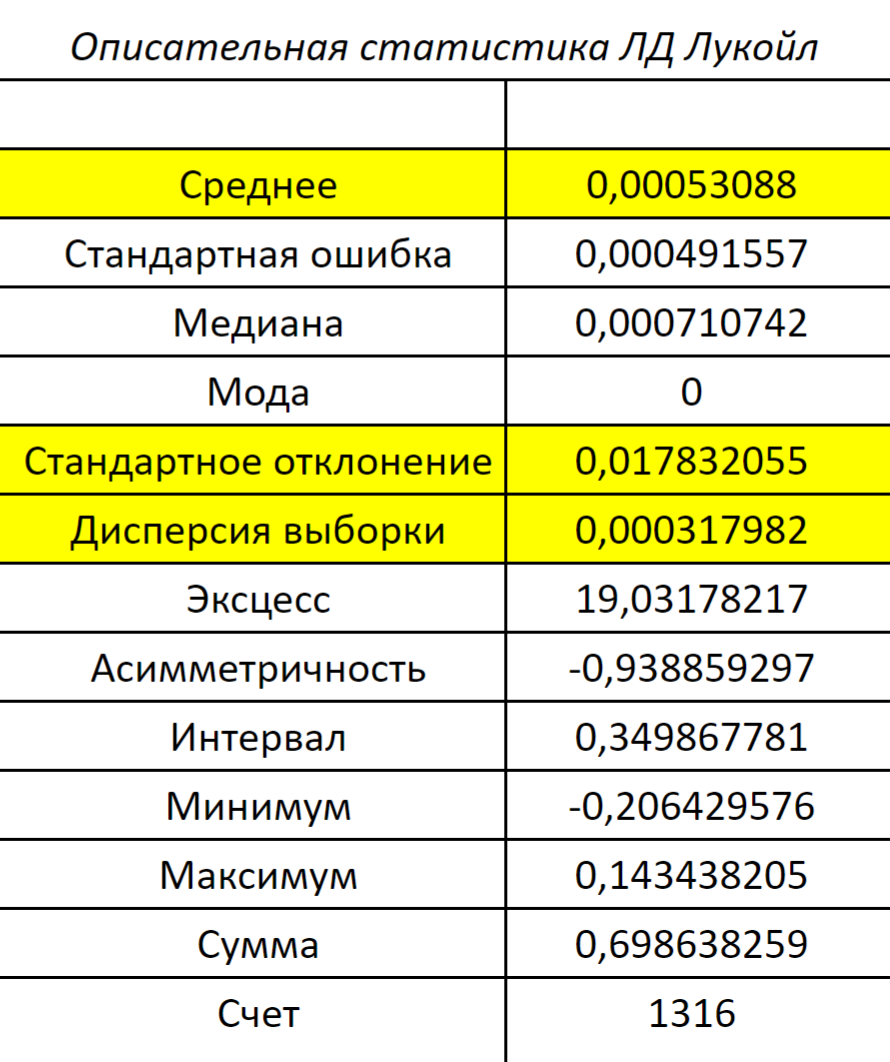
Еще нужно определить, как ценные бумаги взаимосвязаны между собой, то есть узнать их корреляцию.
Для этого воспользуемся встроенной функцией КОРРЕЛ в «Экселе»: раздел «Анализ данных» — «Корреляция».

На выбранном временном отрезке корреляция между акциями «Русгидро» и «Лукойл» составляет 0,32. То есть они связаны положительно — при росте цены одной бумаги вторая тоже покажет рост. Но все же корреляция не такая сильная, как, скажем, у «Лукойла» с другой компанией из нефтегазовой отрасли, например «Роснефтью». Ведь это компании со схожей бизнес-моделью, зависящие от тех же факторов, в частности от котировок на нефть.
А при корреляции 0,32 между «Лукойлом» и «Русгидро» диверсификация будет работать неплохо, так что мы сможем снизить уровень риска портфеля.
Итак, мы посчитали корреляцию между акциями, а также ожидаемую доходность и стандартное отклонение каждой бумаги. Теперь можно перейти к поиску оптимального портфеля.
Поиск самых доходных портфелей. Обратимся к вкладке «Анализ» нашей гугл-таблицы. Соберем различные варианты портфелей из выбранных акций, меняя долю каждой с шагом 10%. То есть портфель № 1 состоит только из акций «Русгидро», портфель № 2 — на 90% из акций «Русгидро» и на 10% из акций «Лукойла» и так далее. Получится 11 портфелей.
Для каждого портфеля рассчитаем его ожидаемую доходность и риск, а именно дисперсию. Для оценки последней задействуем следующую формулу:
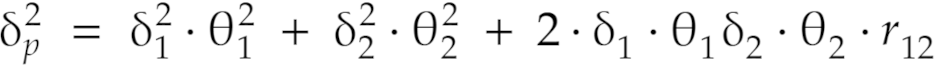
Сигма в этом случае обозначает стандартное отклонение ценной бумаги, а тета — удельный вес ценной бумаги в портфеле, r12 — коэффициент корреляции между ценными бумагами в портфеле.
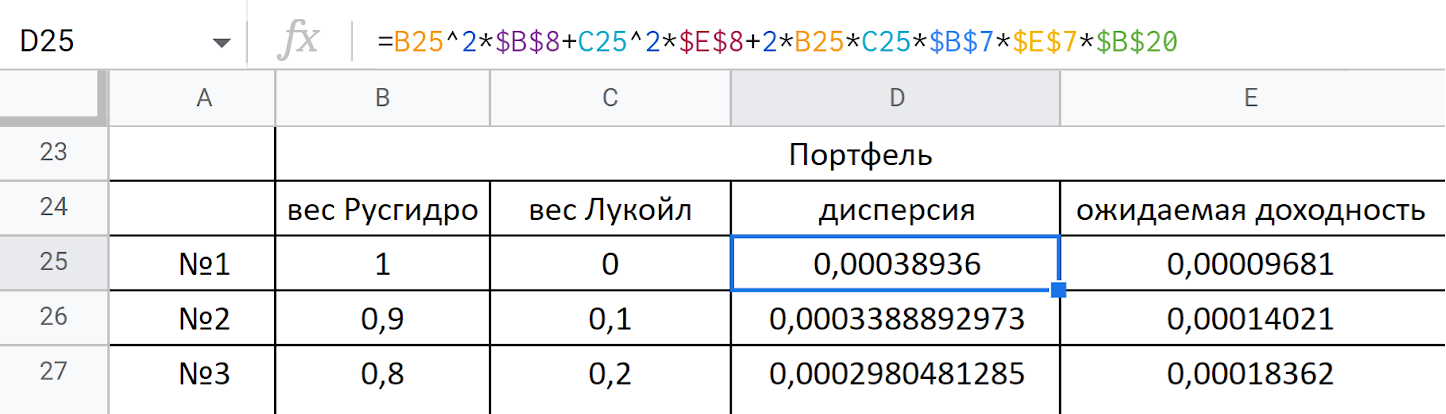
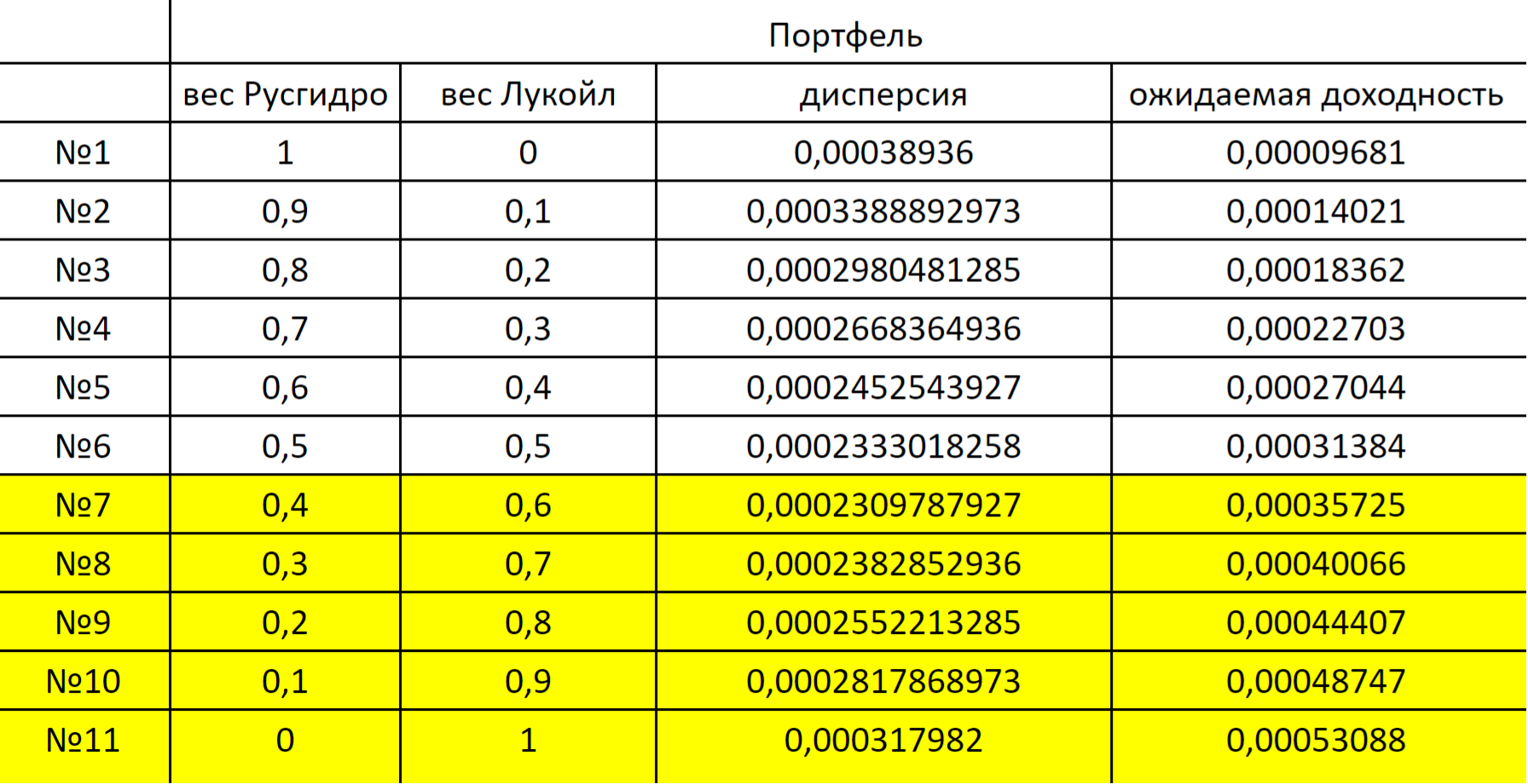
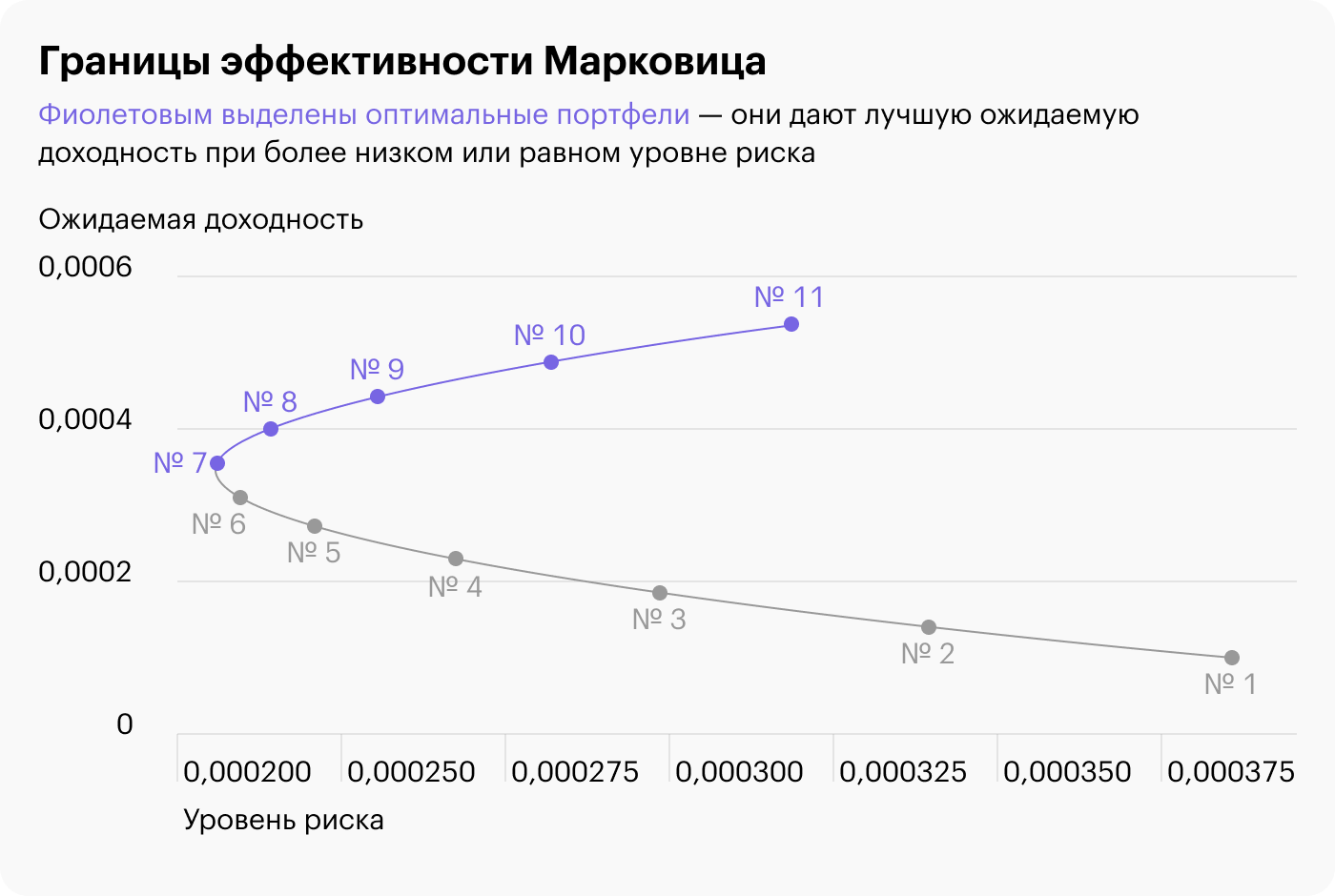
График границы эффективности. По полученным данных построим график, который будет показывать связь риска и доходности каждого портфеля. По оси Y выделяем математическое ожидание, по оси Х — дисперсию портфеля. Ниже представлен получившийся график.
Все оптимальные портфели расположены на синей линии. Любые варианты выше графика недостижимы: не существует портфелей с таким отношением доходности к риску. А портфели ниже графика неэффективны: у них хуже соотношение доходности и риска.
В дальнейшем мы будем использовать только эти оптимальные портфели, а именно № 7, 8, 9, 10, 11.
Составляем матрицу выигрышей на основе критерия эффективности Шарпа
Чтобы оценить, какой из пяти полученных портфелей подходит лучше всего, необходимо задать условия неопределенности. Ведь инвестор всегда действует в таких условиях. Например, он не знает, какими будут через год курс доллара и политическая ситуация в стране.
В нашем примере в качестве условия неопределенности выберем изменчивость показателей во времени: никто не может точно сказать, будет ли в следующем году доходность такой же, как в текущем, и что будет с риском портфеля. Это обычно и волнует инвестора — что показатели доходности и риска со временем могут меняться.
«Условия неопределенности» будем рассматривать на промежутках 2016, 2017, 2018, 2019 годов. А сама неопределенность заключается в том, что мы наверняка не можем знать доходность и риск активов из года в год.
Теперь нам необходимо рассчитать доходность и риск двух ценных бумаг для каждого года, а не за весь период, как делали ранее. Для расчета мы также будем использовать эксель-программу «Описательная статистика» из раздела «Анализ данных». Мы оцениваем данные отдельно за каждый период, чтобы можно было составить матрицу рисков для полноценного использования инструментария теории игр, в частности критериев Вальда и Сэвиджа.
Результаты расчетов представлены на вкладке «Описательные статистики». Там же мы аналогично составим корреляционные матрицы, математическое ожидание и дисперсии для каждого года.
Оценка эффективности. Для оценки эффективности управления портфелем ценных бумаг существует довольно много коэффициентов, но базовые — Шарпа и Трейнора.
Их различие состоит в том, что Шарп в качестве оценки риска использует стандартное отклонение доходности портфеля, а Трейнор — бету портфеля, то есть риск портфеля по отношению к рынку.
Что за коэффициент «бета»
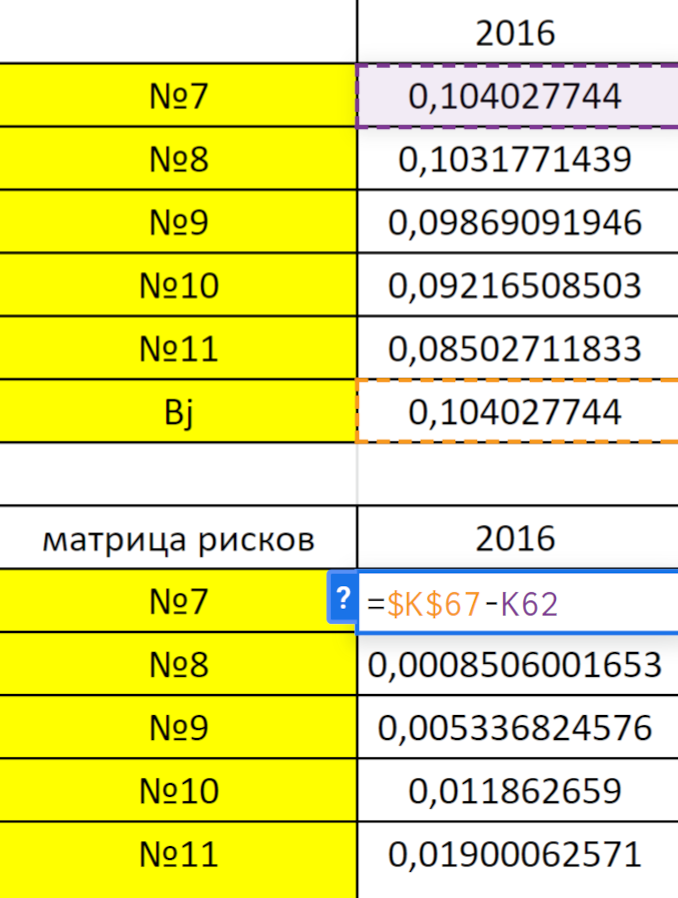
Это статистический параметр, который характеризует направление и амплитуду движения актива относительно широкого рынка. Под последним обычно понимают индекс S&P 500.
Бету могут рассчитывать как для отдельной акции, так и для портфеля в целом. Для этого сравнивают поведение актива с индексом на определенном отрезке времени. Например, Московская биржа ежедневно предоставляет калькуляцию значений коэффициента «бета» для российских эмитентов по итогам 30 торговых сессий.
Значения коэффициента интерпретируются так:
- 0 < бета < 1 — актив движется однонаправленно с индексом, но колеблется не так сильно, риск меньше рыночного.
- −1 < бета < 0 — корреляция между активом и индексом обратная. Они движутся в разные стороны, но актив ведет себя более стабильно.
- Бета < −1 — корреляция обратная, но актив несет в себе больший риск в сравнении с рыночным.
- Бета > 1 — означает, что актив коррелирует с индексом, но ведет себя более волатильно. Актив очень рисковый.
Формулы для расчета данных коэффициентов Шарпа и Трейнора следующие:
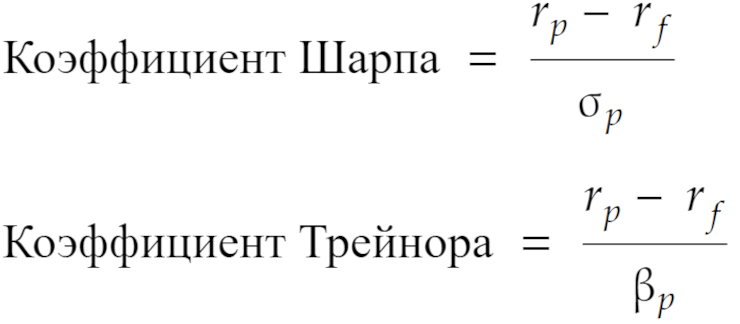
Числители у коэффициентов одинаковы — разница между доходностью портфеля и доходностью безрискового вложения, то есть реальная доходность от инвестиций. А в знаменателе учитывается риск, который мы на себя приняли.
Эти коэффициенты показывают, сколько пунктов доходности мы получили на единицу риска.
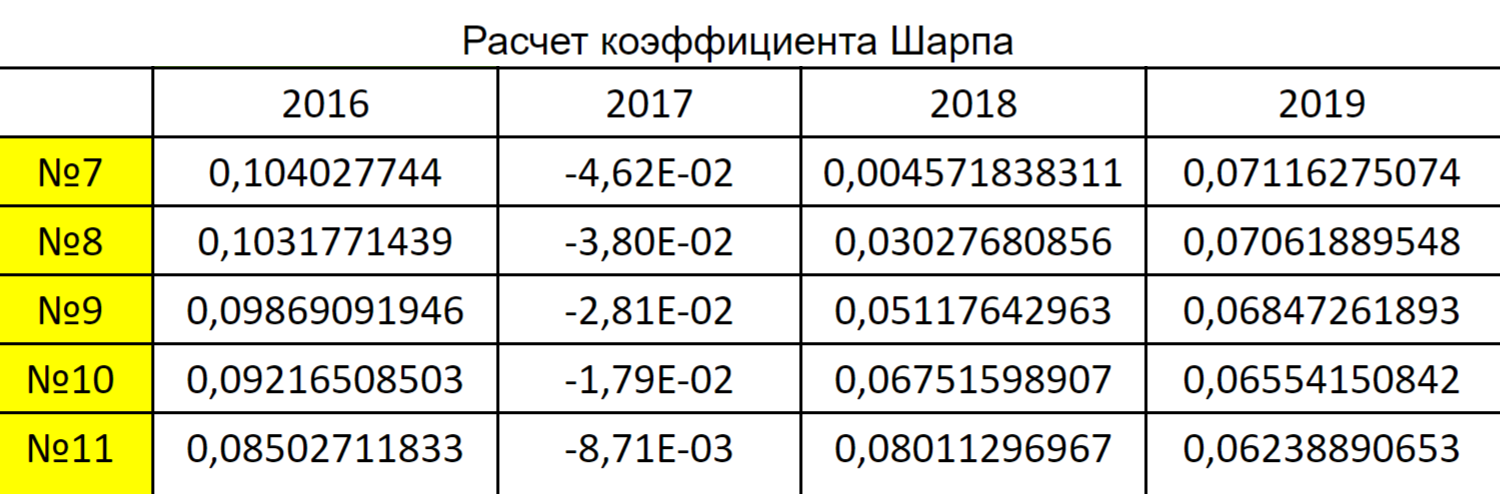
Воспользуемся коэффициентом Шарпа, так как в качестве меры риска мы выбрали стандартное отклонение доходности акций. Рассчитаем его для каждого из пяти оптимальных портфелей для каждого года.
Получившаяся таблица — лишь промежуточные данные, которые понадобятся для дальнейших расчетов, а именно при расчете критериев Вальда и Сэвиджа. О них пойдет речь ниже.
В каждой ячейке таблицы содержатся данные о коэффициенте Шарпа для определенного портфеля в определенном году.
Ищем показатели эффективности по критерию Вальда
Синтетический критерий Вальда — Сэвиджа — популярный метод нахождения оптимальных стратегий в теории игр. Он позволяет в полной мере отразить портфельную теорию Марковица, так как связывает выигрыши игрока в условиях неопределенности с его рисками. Рассмотрим критерии Вальда и Сэвиджа более детально.
Критерий Вальда. Определяет оптимальность стратегии с позиции выигрыша. Суть критерия Вальда такой: он обеспечивает максимальный среди минимальных выигрышей. Например, если есть три безрисковых портфеля, мы выберем тот, что имеет наибольшую доходность. Здесь можно провести аналогию с эффективной границей Марковица.
В итоге мы должны получить «гарантированный результат» — тот, на который рассчитывает инвестор независимо от неопределенности на рынке. Поэтому в литературе критерий Вальда также называют принципом гарантированного результата.
Эта методика отлично подходит, если инвестор консервативен по отношению к риску, то есть не гонится за высокой доходностью и не хочет принимать на себя лишние риски. Его задача — сохранить сбережения и при этом немного заработать.
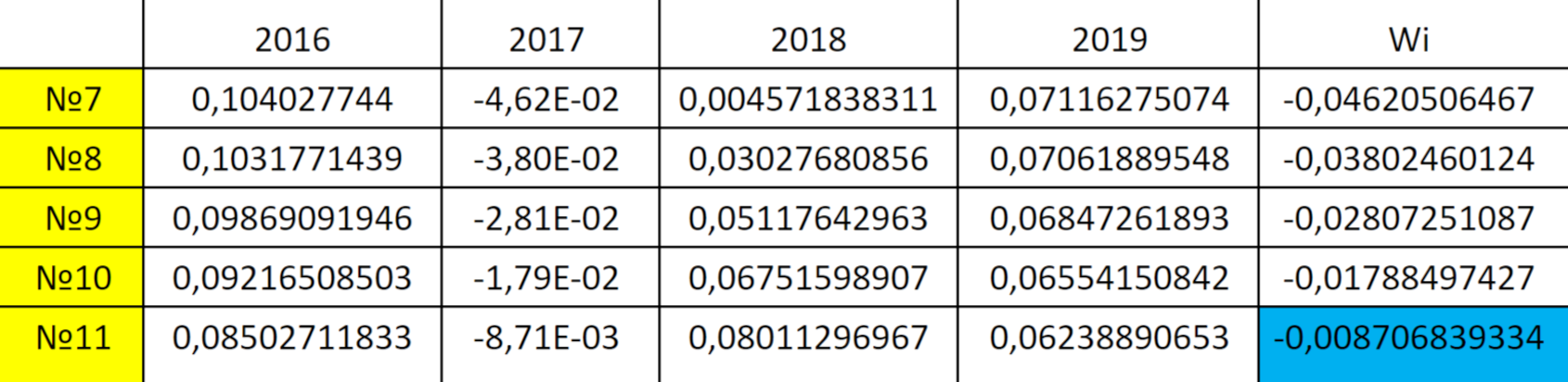
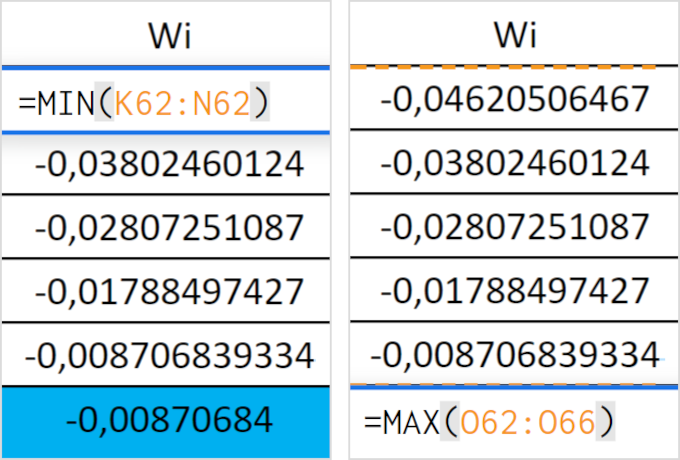
Критерию Вальда соответствует столбец Wi в таблице ниже: сначала оцениваем минимальные выигрыши по каждому портфелю, а затем берем максимальный среди этих минимальных. Такое значение помечено синим цветом. Оно соответствует портфелю № 11.
Критерий Сэвиджа. С другой стороны, оптимальной стратегией для инвестора по критерию Сэвиджа будет та, что обеспечит минимальный среди максимальных рисков. Этот критерий еще называют критерием крайнего пессимизма.
Инвестор изначально ориентируется на портфели, которые обеспечивают ему максимальный риск. Таким образом, критерии Вальда и Сэвиджа по своей сути противоположны друг другу.
Критерий Вальда оценивает ситуацию с точки зрения выигрышей инвестора, а критерий Сэвиджа — с точки зрения рисков инвестора. В обоих случаях реализуется концепция Марковица «риск — доходность».
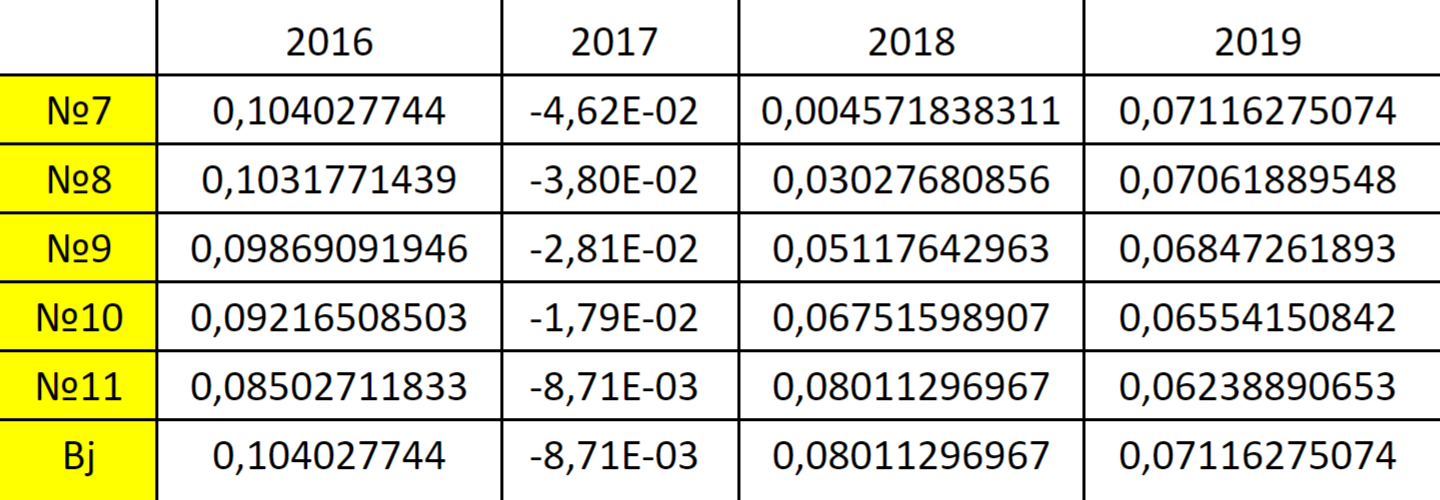
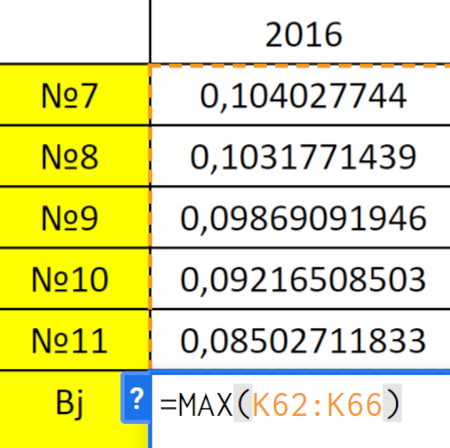
Чтобы воспользоваться критерием Сэвиджа, необходимо рассчитать максимальное значение коэффициента Шарпа для каждого периода. Расчеты представлены в строке Вj таблицы ниже. Это промежуточные данные, которые нам понадобятся на следующем шаге.
Считаем матрицу рисков и определяем цену игры по критерию Сэвиджа
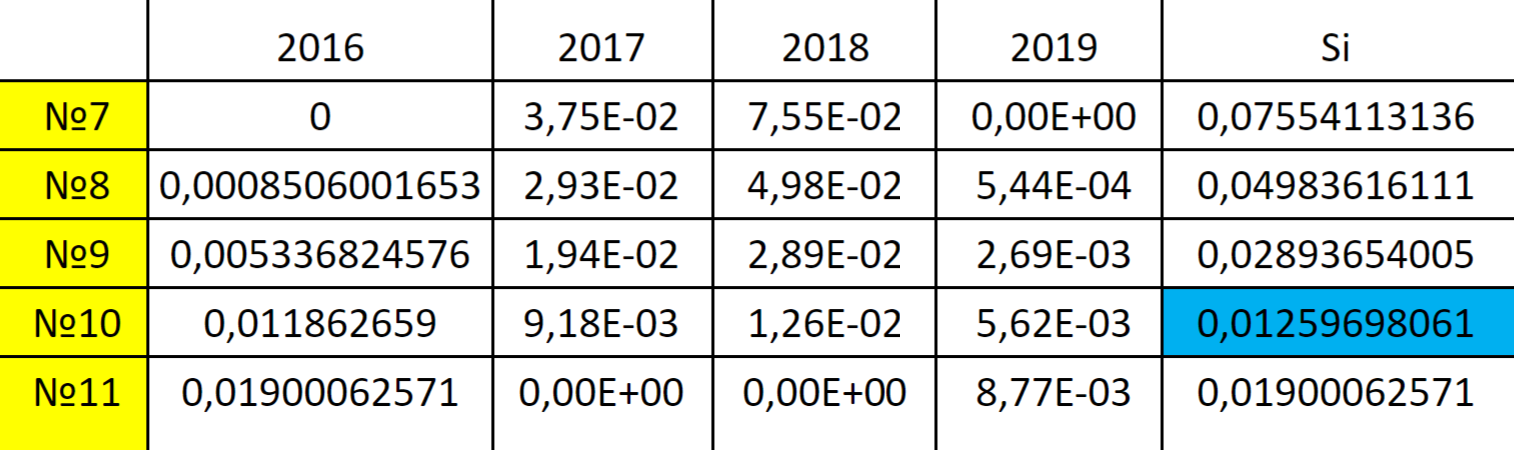
Далее необходимо составить матрицу рисков, чтобы мы могли воспользоваться критерием Сэвиджа. Риск в этом случае — отклонение коэффициента Шарпа от своего максимального значения за рассматриваемый период. Другими словами, это риск недополучения доходности.
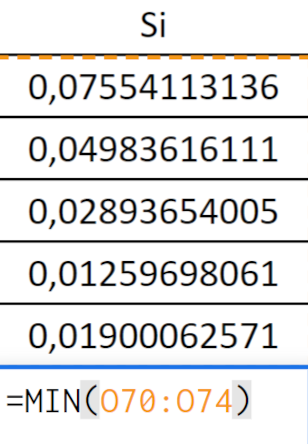
В итоге по критерию Сэвиджа мы выбираем минимальный риск среди максимальных. Это значение соответствует портфелю № 10.
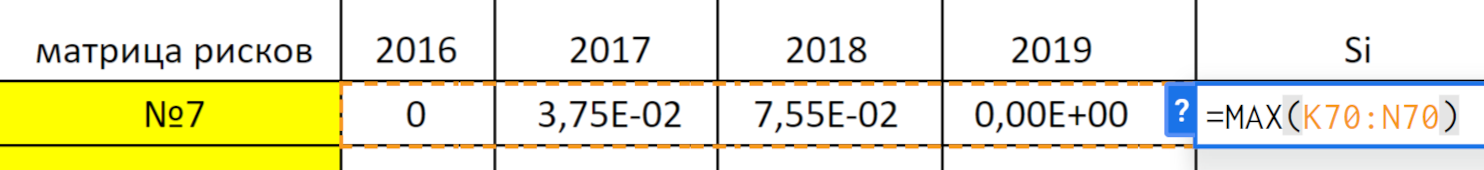
Связать критерии Вальда и Сэвиджа
Теперь нам нужно связать критерии Вальда и Сэвиджа и, соответственно, полученные данные. Линейная комбинация двух критериев позволяет оценить инвестиционный портфель с точки зрения модели «риск — доходность».
Введем уравнение, связывающее два этих показателя. В качестве коэффициента возьмем r, которое задается инвестором и отражает степень его подверженности риску.
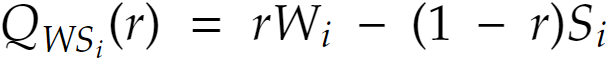
В формуле Wi — показатель эффективности стратегии Ai по критерию Вальда; Si — показатель эффективности стратегии Ai по критерию Сэвиджа, i ∈ I.
Чтобы проранжировать инвестиционные портфели по степени их привлекательности в зависимости от заданного значения r, нужно построить таблицу показателей эффективности для крайних его значений, то есть при r = 0 и r = 1. Значению 0 соответствует абсолютно консервативный профиль инвестора, который совершенно не желает рисковать. При r = 1 мы можем судить об агрессивном инвесторе, который никак не защищается от рисков.
Рассчитаем показатели эффективности по указанной выше формуле.

Чтобы понять, пересекаются портфели или нет, необходимо смотреть на пограничные значения при r = 0 и r = 1. Если в каком-то портфеле при r = 0 значения выше, чем у другого, а при r = 1, наоборот, ниже — это значит, что портфели пересекаются.
В нашем случае такая ситуация наблюдается только между портфелями № 10 и 11. При r = 0 значение № 11 меньше значения № 10, а при r = 1 значение № 11 больше значения № 10.
Ранжирование портфелей по степени привлекательности будет зависеть от r — склонности инвестора к риску. Уточню, что на этом этапе мы рассматриваем портфели с точки зрения приоритетности для инвестора. То есть при заданном уровне риска выбираем последовательность портфелей от лучшего к худшему.
Определяем приоритетную последовательность инвестиционных портфелей
Найдем точку пересечения портфелей и проранжируем их. На картинке ниже видно, что портфели № 10 и 11 пересекаются ориентировочно при r = 0,41.
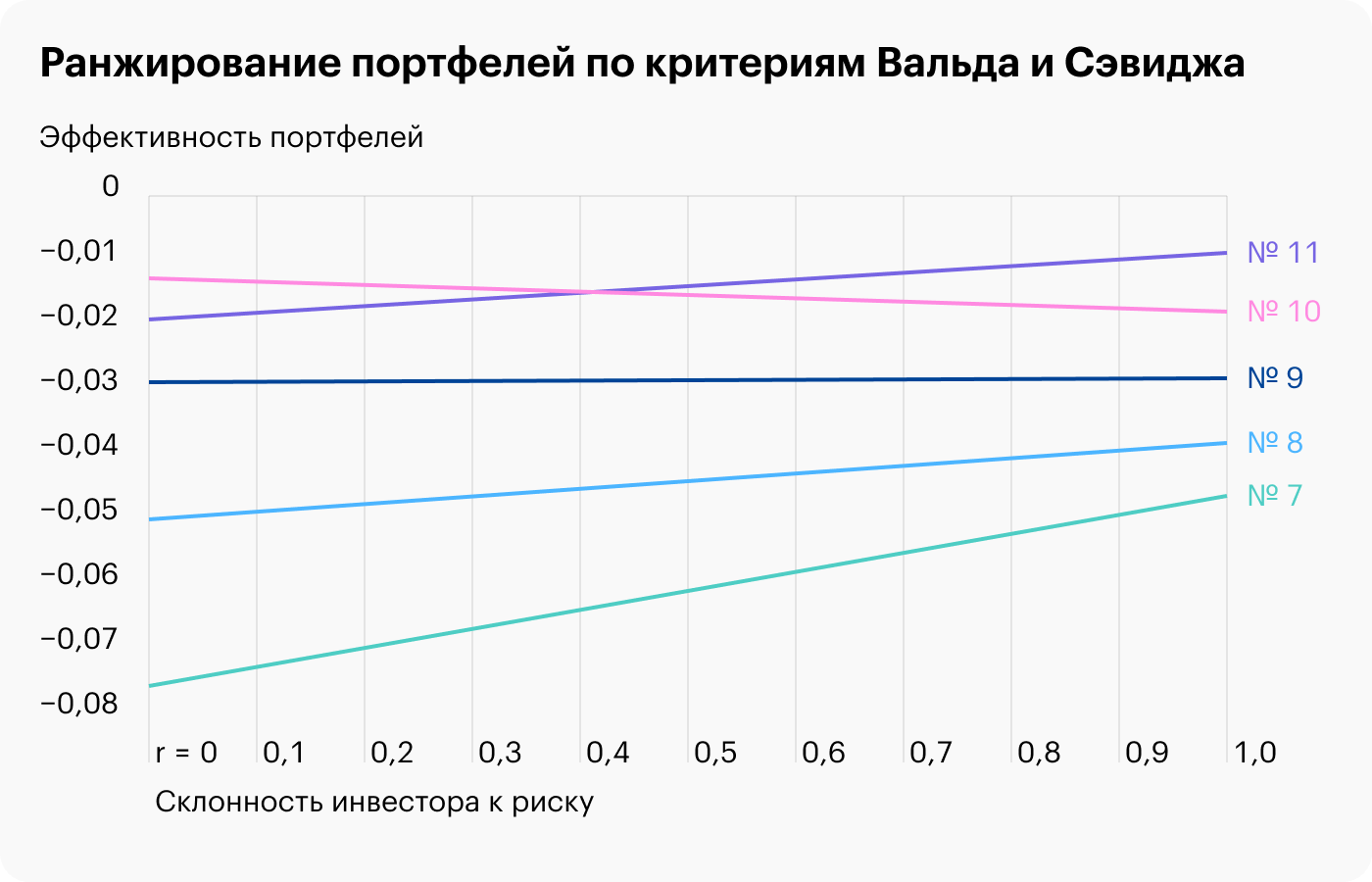
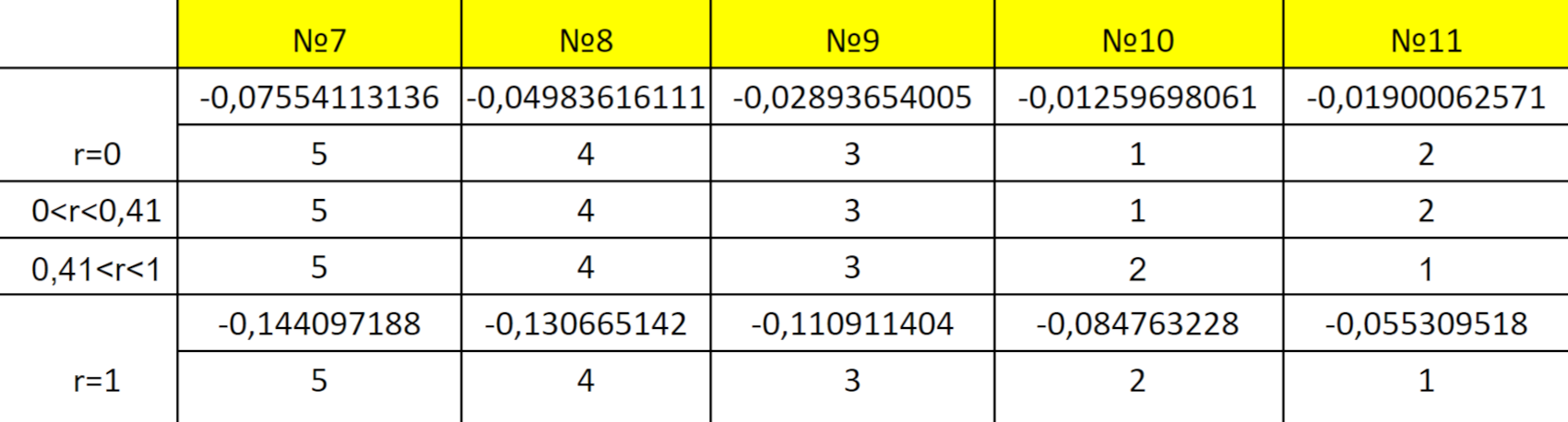
Как видно из результатов ранжирования, степень привлекательности портфеля зависит от значения r — степени подверженности к риску.
Условно можно выделить три типа инвесторов:
- 0 < r < 0,25 — консервативные инвесторы.
- 0,25 < r < 0,6 — умеренно-агрессивные инвесторы.
- 0,6 < r < 1 — агрессивные инвесторы.
В нашем случае, если инвестор консервативен или в небольшой степени разбавляет портфель волатильными бумагами, то есть его склонность к риску от 0 до 0,41, ему следует выбрать портфель № 10: 10% акций «Русгидро» и 90% акций «Лукойла».
Если подверженность инвестора к риску умеренная или агрессивная, то предпочтительнее портфель № 11, состоящий исключительно из акций «Лукойла».
Таким образом, на конкретном примере мы определили набор оптимальных стратегий инвесторов на основе подхода Марковица. Затем, используя математический аппарат теории игр, а точнее синтетический критерий Вальда — Сэвиджа, установили приоритетный порядок инвестиционных портфелей в зависимости от значения r — степени принятия инвестором риска.
Запомнить
- Диверсификация портфеля — ключевая методика, которая позволяет сгладить волатильность портфеля и практически полностью устраняет специфические риски, связанные с конкретными эмитентами.
- Для диверсификации лучше всего подходят активы, которые слабо или отрицательно коррелируют между собой. Например, исторически неплохим диверсификатором для американских акций выступают казначейские облигации и золото.
- Коэффициенты Шарпа и Трейнора показывают эффективность портфеля — какую доходность дает портфель на единицу риска.
- Синтетический критерий Вальда — Сэвиджа позволяет связать два ключевых параметра на финансовом рынке: риск и доходность.
- Суть критерия Вальда — обеспечение максимального среди минимальных выигрышей.
- По критерию Сэвиджа оптимальной стратегией для инвестора будет та, что обеспечивает минимальный среди максимальных рисков. Это критерий крайнего пессимизма.
- С помощью критерия Вальда — Сэвиджа мы определяем приоритетную последовательность портфелей для определенного типажа инвестора, в зависимости от его склонности к риску.
Хотите написать такую статью для Т—Ж? Любой процесс, в котором в каком-то виде участвуют деньги, можно превратить в тему для Т—Ж. Прочитайте наш мануал для авторов и приносите заявку на статью.



























